​ ok. 8 minuty czytania - polub, linkuj, komentuj!

---

Asumpt do rozważań nad algorytmami i heurystykami

„Coraz częściej obserwuję na szkoleniach oczekiwanie uczestników dotyczące wskazania konkretnego sposobu działania, czyli algorytmu” – twierdzi Sławomir Łais w jednym ze swoich wpisów na EPALE. Z tekstu wynika, że osoby biorące udział w szkoleniach liczą na to, że pozyskane umiejętności pozwolą im bezbłędnie rozwiązywać bazowe dla tematu zajęć problemy dzięki znajomości schematycznej ścieżki prowadzącej niezawodnie od punktu wyjścia do punktu dojścia, czyli satysfakcjonującego rozwiązania. Innymi słowy oczekują poznania algorytmu właśnie. Rolą edukatora zaś jest przygotowanie jasnego diagramu opisującego wszystkie możliwe węzły decyzyjne i przekazanie go w jak najbardziej dostępnej formie.

Doskonale to zapotrzebowanie rozumiem, po pierwsze dlatego, że bezustannie się z nim w pracy edukacyjnej spotykam, a po drugie, sam czegoś się ucząc, często poszukuję podobnych ścieżek. Niemniej by sprawiedliwie oddać sensowność tworzenia algorytmów, myślę, że zachwyt wobec nich, który przytoczony artykuł mógłby wywołać, należy nieco ostudzić, wskazując na pewne okoliczności, które poniżej opisuję. Mój tekst jest raczej addendą do tekstu Sławomira niż polemiką.

Rozpocznę od rozwinięcia tego, czym jest algorytm, posługując się konkretnym przykładem.

Gra w piętnastkę – przykład algorytmu

Piętnastka to prosta gra karciana. Wystarczy do niej 9 kart jednego koloru od asa (wartość 1) do dziewiątki. Dwóch graczy naprzemiennie wybiera po jednej karcie. Ten, któremu jako pierwszemu uda się zebrać takie karty, że dokładnie trzy z nich mają łączną wartość 15, wygrywa. 

Weźmy konkretny przykład. Rozpoczyna przeciwnik i wybiera szóstkę. Teraz Twój ruch. Zachęcam do krótkiej pauzy i zastanowienia (właściwa odpowiedź znajduje się nieco dalej). Domyślasz się zapewne, że Twój wybór jest nie bez znaczenia. Jeśli gra jest sprawiedliwa, musi istnieć droga, która pozwoli Ci wygrać lub przynajmniej nie przegrać. Jednak masz aż osiem możliwych opcji, a to dopiero pierwszy ruch. Co prawda w następnym będzie już mniej kart, więc i możliwości mniej, ale łączna liczba potencjalnych rozgrywek to iloczyn ilości opcji w kolejnych rundach. Co więcej, przeciwnik również ma swobodę wyboru, więc gdyby chcieć obliczyć ilość wszystkich scenariuszy, należałoby pomnożyć 9*8*7*6… i tak aż do chwili, gdy ktoś wygrywa. Niemniej po takim początku istnieje tylko jeden poprawny ruch, który nie daje przeciwnikowi przewagi.

Algorytm w tej grze to kompletny system kroków, które należy podjąć w każdej kolejnej rundzie, uwzględniający poczynania przeciwnika, który to system pozwoli nie przegrać, a w przypadku błędu przeciwnika nawet wygrać w tej grze. Taki algorytm w piętnastce istnieje, niemniej łatwo zauważyć, że choć gra jest dość prosta, to algorytm wcale nie musi być łatwy do zapamiętania. Tymczasem na ogół, grając w inne gry karciane, dysponujemy pełną talią (ba, nawet czasem dwiema), część kart jest zakrytych, a reguły niejednokrotnie bardziej zawiłe niż uzbieranie trzech kart o określonych właściwościach. Czy wówczas ktokolwiek jest w stanie opanować algorytm poprawnej gry? Do problemu piętnastki jeszcze wrócę.

Czym jest heurystyka

Obecna moc obliczeniowa komputerów zmienia nasze spojrzenie na algorytmy, niemniej w przypadku ludzkiej pamięci i sprawności intelektualnej gry typu szachy nie da się opisać za pomocą algorytmów. Co prawda doniesienia medialne informują, że arcymistrzowie światowi są w stanie przewidywać nawet 30 ruchów, niemniej to wciąż za mało, aby zakończyć każdą partię, nie mówiąc już o tym, że jest to poziom geniusza, zupełnie niedościgły dla przeciętnego szachisty. Dlatego ucząc się grać w szachy, przyjmuje się pewne zasady, które dość łatwo opanować, a które podnoszą ogólny poziom gry. Jedną z nich może być ocena punktowa wartości poszczególnych figur i bierek od hetmana poprzez wieże, laufry i skoczki do pionów. Jeśli w wyniku bicia przeciwnik traci figurę silniejszą (o wyższej wartości) niż ja, to na ogół zyskuję. Zatem, kiedy mam okazję do wykonania ruchu zgodnie z tą zasadą, powinienem tak postąpić. To jest właśnie heurystyczne rozwiązywanie problemu. Innym przykładem heurystyki może być ustawianie pionów w nieprzerwanym szeregu albo wzmożona uwaga na szczególnie wrażliwe pola szachownicy (jak np. F7).

W miarę wprawny gracz szybko zauważy, że dobrze usytuowany skoczek potrafi więcej zdziałać niż zablokowana w kącie wieża. I to prawda. Dlatego muszę zaznaczyć, że heurystyka bywa zawodna. Znajdziemy wiele wyjątków od reguły ją stanowiącej.

Posłużę się jeszcze jednym przykładem. Oto zadanie: spośród wszystkich par liczb dających w iloczynie 12 znaleźć te, które sumują się do siedmiu. Jest to proste zadanie matematyczne na poziomie liceum. Jak będzie wyglądać algorytm rozwiązania? Wystarczy napisać układ równań:

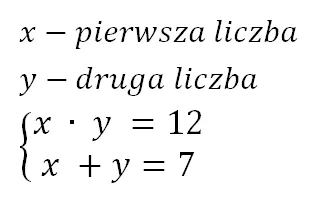
Ponieważ jedno z równań jest nieliniowe, zadanie daje się sprowadzić do równania kwadratowego z jedną zmienną. A potem już wiadomo, obliczamy deltę i dwa pierwiastki.

A co gdyby zastosować heurystykę? Bądź co bądź do tych wszystkich obliczeń potrzebny jest pewnie papier i ołówek oraz bezbłędna znajomość wzorów, które przypuszczalnie niektórzy chętnie by już wyrzucili ze swojej pamięci, a przecież rozwiązanie wydaje się proste, ot na wyciągnięcie ręki. Spróbujmy skonstruować zatem jakąś heurezę. Pomysł mam taki, aby pary liczb poszukać wśród dzielników liczby 12 i to najlepiej dodatnich, żeby się nie przemęczać minusami. Par liczb całkowitych dających po pomnożeniu 12 znajduję trzy, są to 1 i 12, 2 i 6 oraz 3 i 4. Czy któraś daje w sumie siedem? Nie trzeba zbyt skomplikowanych obliczeń ani nawet zapisu na kartce, by wskazać prawidłowe rozwiązanie. Są to liczby 3 i 4. Tadam! 

Po co zatem uczymy się tych wszystkich skomplikowanych wzorów w szkole? Otóż odpowiedź jest dość oczywista. Wystarczy, że liczby mają zsumować się np. do dziewięciu. Wówczas nie otrzymamy „ładnych” liczb całkowitych, ale „brzydkie” liczby niewymierne. Niemniej algorytm się nie zmieni. Ba, nawet zaoszczędzimy czas na skracaniu ułamków w którymś miejscu. Tymczasem moja heurystyka zupełnie nie działa. Powiem więcej, trudno wymyślić rozumowanie prostsze od algorytmu, które doprowadzi do prawidłowego rozwiązania.

Widać zatem, że choć myślenie heurystyczne może uprościć problem i przyspieszyć działanie, to jednak bywa zawodne.

Gra w piętnastkę – przykład heurystyki

Wróćmy do gry w piętnastkę z początku tekstu. Kiedy pierwszy raz spotkałem się z tą grą, miałem ambiwalentne odczucia. Po pierwsze, od razu poczułem energię do tego, by stworzyć algorytm właściwego postępowania w kolejnych ruchach – wszak to pobudzające ćwiczenie intelektualne! Jednak z drugiej strony, szybko się zorientowałem, że jestem zbyt leniwy, by swoje konstruujące się w głowie dzieło zapamiętać i z powodzeniem stosować. Niemniej samo zastanawianie się nad problemem przyniosło pewne nieoczekiwane rezultaty. Gdzieś w myślach pojawiły się takie właściwości problemu jak symetria, karty parzyste, karty nieparzyste, ilość rozwiązań. Nie umiem dokładnie opisać, jak do tego doszło, ale ostatecznie po dłuższym namyśle przyszło mi do głowy skojarzenie z grą, którą doskonale znałem – mianowicie kółko i krzyżyk. Jeszcze wówczas nie byłem pewny sensowności swojego pomysłu, ale szybko rozrysowałem popularny diagram trzy na trzy pola, wpisując w kolejnych rzędach dziewięć wartości kart – w pierwszym: 2, 7, 6; drugim: 9, 5, 1 i ostatnim 4, 3, 8. Od teraz wystarczy grać w kółko i krzyżyk!

Co prawda malkontenci podkreślą, że przecież w tej grze aby wygrać, nadal należy posłużyć się algorytmem. To prawda, ale po pierwsze, ten algorytm już znałem, więc dla mnie to spory zysk, bo nie muszę się uczyć nowego. Po drugie zaś, ujęcie graficzne niezbicie ukazuje, że diagram można dowolnie obracać o 90, 180 czy 270 stopni, a gra się nie zmieni, więc jest to zasadniczo algorytm dość prosty. Natomiast droga, jaką myślowo przeszedłem od piętnastki do zastąpienia ją kółkiem i krzyżykiem, jest właśnie heurystyką.

Wracając do problemu z początku tekstu, można zauważyć, że po zabraniu przez przeciwnika szóstki w pierwszym ruchu, trzeba szybko zagarnąć piątkę! To jedyny ruch, który nie daje rywalowi przewagi, co zauważył już pewnie każdy wprawny gracz w kółko i krzyżyk. Po zagraniu rywala w narożniku trzeba niezwłocznie zająć środek.

Problemy zamknięte i otwarte

Zupełnie do tej pory nie poruszyłem jeszcze jednej, być może najbardziej zasadniczej okoliczności stosowania algorytmów i heurystyk. Dotąd wszystkie moje przykłady zakładały, że istnieje jakieś rozwiązanie lub zbiór rozwiązań, które obiektywnie da się ocenić jako poprawne, wszystkie pozostałe natomiast są błędne. Wiele problemów z naszego świata rzeczywiście cechuje ta właściwość. Wspomniany przez Sławomira Łaisa casus regulacji RODO jest pewnie jednym z nich. Niemniej nie jest to cecha uniwersalna. Co więcej, w dziedzinach takich jak edukacja, komunikacja, polityka i wielu innych na ogół problemy nie mają jednoznacznie poprawnego lub bezsprzecznie złego zbioru rozwiązań. Na ogół musimy zaakceptować fakt, że istnieje (być może nieskończenie) wiele alternatywnych rozwiązań, do których nie prowadzi żadna bezdyskusyjna ścieżka. Tę pierwszą klasę przypadków nazywamy problemami zamkniętymi, tę drugą otwartymi. Niestety w otwartych nie da się budować algorytmów (a przynajmniej nie w takim celu, o jakim mówimy). Dlatego na ogół posługujemy się heurystykami. Na przykład zasady kształcenia są właśnie takimi heurystykami (zasada poglądowości, zasada trwałości wiedzy, zasada systematyczności itd.). Nie da się ich stosować jak swego rodzaju gotowca do prowadzenia zajęć, niemniej pomagają w ułożeniu programu kursu czy scenariusza spotkania.

Algorytm czy heurystyka – porównanie

W poniższej tabeli zestawiam najważniejsze cechy rozwiązywania problemów za pomocą algorytmów i heurystyk.

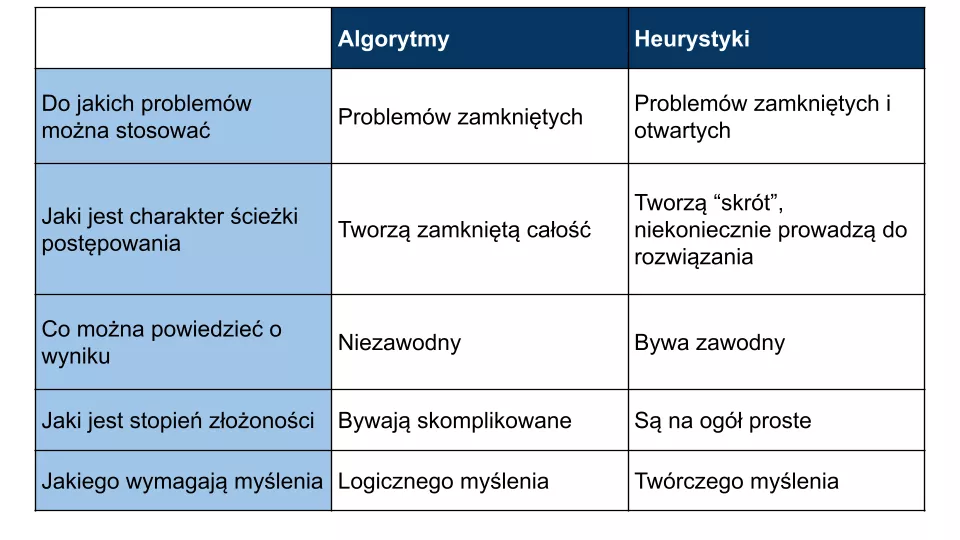
Bardzo ciekawym zagadnieniem byłoby, jak uczyć myślenia heurystycznego (bo algorytmicznego uczymy choćby przez 12 lat obowiązkowej matematyki w szkole), ale to już temat na innego bloga. 

Zadanie dla Czytelników – Nim

Na koniec wyzwanie dla chętnych. Nim jest starochińską grą o następujących zasadach:

1. Jest to gra dla dwóch graczy.
2. Do gry można wykorzystać dowolną ilość podobnych przedmiotów, np. zapałek, kapsli, monet lub muszelek czy guzików.
3. Wszystkie przedmioty dzielimy na trzy stosy. Ilość przedmiotów w stosie jest dowolna, niemniej wskazane jest, aby na każdym było co najmniej kilka i aby było łatwo je policzyć.
4. Gracze wykonują ruchy naprzemiennie.
5. Podczas swojego ruchu gracz może wziąć dowolną liczbę przedmiotów, ale tylko z jednego stosu. Można wziąć nawet cały stos. Trzeba wziąć przynajmniej jeden przedmiot.
6. Przegrywa gracz, który wziął ostatni przedmiot.

Jeśli na poszczególnych stosach będzie leżeć kolejno: cztery, pięć i sześć przedmiotów, to jaki ruch należy wykonać (ile wziąć przedmiotów i z którego stosu), aby wygrać? Są tylko trzy ruchy, które pozwalają iść po zwycięstwo bez względu na decyzje przeciwnika. Pozostałe (a wszystkich dostępnych ruchów w tej turze jest piętnaście) zsyłają nas na łaskę lub błąd przeciwnika.

Osoba, która jako pierwsza w komentarzu poniżej wymieni wszystkie trzy alternatywne ruchy, dostanie prawo wyboru tematu mojego kolejnego wpisu na blogu, a w puli są:

1. Cykl uczenia się według Marilyn Taylor; 
2. „Wild West Jungle” – recenzja gry szkoleniowej;
3. Przykład ciekawej gry szkoleniowej ujawniającej wyłanianie się lidera grupy.

Na odpowiedzi czekam do 15 września 2022 (mam nadzieję, że nie za trudne dałem zadanie).

---

dr Wojciech Świtalski – pedagog, andragog, adiunkt w Katedrze Andragogiki i Gerontologii Społecznej Uniwersytetu Łódzkiego. Specjalizuje się w metodyce kształcenia w środowisku szkolnictwa wyższego i edukacji dorosłych, zwłaszcza z wykorzystaniem gier i zabaw. Sprawny organizator licznych wydarzeń edukacyjnych. Ambasador EPALE.

---

Zobacz także:

Moje wrażenia z IV Ogólnopolskiego Zjazdu Andragogicznego

Karty coachingowe – recenzja wybranych narzędzi

Uczenie się w świetle konstruktywizmu społecznego na przykładzie gry "Tajemnicze domostwo"

Style uczenia się